抛物线 $y = {x^2}$ 在 $x = 1$ 处的切线与两坐标轴围成三角形区域为 $D$（包含三角形内部和边界）．若点 $P\left(x,y\right)$ 是区域 $D$ 内的任意一点，则 $x + 2y$ 的取值范围是 ．
【难度】
【出处】
2013年高考江苏卷
【标注】
【答案】
$\left[ { - 2,\dfrac{1}{2}} \right]$
【解析】
先利用导数求出抛物线的切线，然后画出可行域，再将目标函数看成直线 $y=-\dfrac12x+\dfrac12z$，只需求直线纵截距 $\dfrac12$ 的范围即可．可求得抛物线 $y = {x^2}$ 在 $x = 1$ 处的切线为\[y=2x-1.\]它与两坐标轴围成的三角形区域如图所示：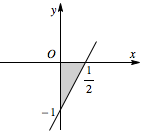
则根据线性规划知识可求得 $x+2y$ 的取值范围为 $\left[-2,\dfrac 12\right]$．
则根据线性规划知识可求得 $x+2y$ 的取值范围为 $\left[-2,\dfrac 12\right]$．
题目
答案
解析
备注
