设 $D,E$ 分别是 $\triangle ABC$ 的边 $AB$,$BC$ 上的点,$AD = \dfrac{1}{2}AB$,$BE = \dfrac{2}{3}BC$,若 $\overrightarrow {DE} = {\lambda _1}\overrightarrow {AB} + {\lambda _2}\overrightarrow {AC}$(${\lambda _1},{\lambda _2} $ 为实数),则 ${\lambda _1} + {\lambda _2}$ 的值为 .
【难度】
【出处】
2013年高考江苏卷
【标注】
【答案】
$\dfrac{1}{2}$
【解析】
根据题中条件,以 $\overrightarrow{AB}$ 和 $\overrightarrow{AC}$ 为一组基底,表示向量 $\overrightarrow{DE}$ 即可.根据题意,$\overrightarrow {DE}=\overrightarrow {DB}+\overrightarrow {BE}=\dfrac 12\overrightarrow {AB}+\dfrac 23\left(\overrightarrow {AC}-\overrightarrow {AB}\right)=-\dfrac 16\overrightarrow {AB}+\dfrac 23\overrightarrow {AC}$.所以 $\lambda_1=-\dfrac 16$,$\lambda_2=\dfrac 23$.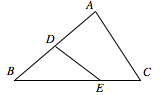

题目
答案
解析
备注