查看数据源：599165c42bfec200011e08f3
在平面直角坐标系 $xOy$ 中，椭圆 $C$ 的标准方程为 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left(a > b > 0\right)$，右焦点为 $F$，右准线为 $l$，短轴的一个端点为 $B$，设原点到直线 $BF$ 的距离为 ${d_1}$，$F$ 到 $l$ 的距离为 ${d_2}$，若 ${d_2} = \sqrt 6 {d_1}$，则椭圆 $C$ 的离心率为 ．
【难度】
【出处】
2013年高考江苏卷
【标注】
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的定义
    >
    椭圆的焦准定义
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的几何量
    >
    椭圆的基本量
【答案】
$\dfrac{\sqrt 3 }{3}$
【解析】
本题考查椭圆的第二定义及椭圆离心率的求法．只需根据题意将题中等式关系转化为 $a,b,c$ 的关系式即可．由题可得，$OB=b$，$OF=c$，$BF=a$，所以 $d_1=\dfrac{bc}{a}$．而椭圆的右准线方程为 $x=\dfrac {a^2}c$，所以 $d_2=\dfrac{a^2}{c}-c$．由 $d_1=\sqrt 6d_2$ 得\[\dfrac{a^2}{c}-c=\sqrt 6\dfrac {bc}a.\]结合 $a^2=b^2+c^2$ 得 $\mathrm e=\dfrac ca=\dfrac {\sqrt 3}3$．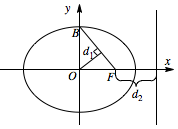 
题目 答案 解析 备注
0.113262s