如图，以过原点的直线的倾斜角 $\theta $ 为参数，则圆 ${x^2} + {y^2} - x = 0$ 的参数方程为 ．
【难度】
【出处】
2013年高考陕西卷（理）
【标注】
【答案】
${\begin{cases}
x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}}$（$\theta $ 为参数）
x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}}$（$\theta $ 为参数）
【解析】
在三角形 $OPM$ 中，利用参数将 $P$ 的坐标表示出来即可，注意分类讨论．将 ${x^2} + {y^2} - x = 0$ 配方，得：\[{\left( {x - \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{1}{4}.\]所以圆的直径为 $ 1 $，设圆上一点 $P\left( {x,y} \right)$，设圆与 $x$ 轴的另一个交点为 $M$，连接 $PM$，则 $\left|OM\right|=1$．
当 $P$ 在 $x$ 轴上方时，\[\begin{split} x &= \left| {OP} \right|\cos \theta \\& = \left|OM\right| \times \cos \theta \times \cos \theta \\& = {\cos ^2}\theta, \\ y &= \left| {OP} \right|\sin \theta \\& = \left|OM\right| \times \cos \theta \times \sin \theta \\& = \sin \theta \cos \theta ,\end{split} \]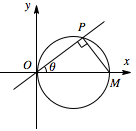
当 $P$ 在 $x$ 轴下方时，\[\begin{split} x &= \left| {OP} \right|\cos \left({\mathrm \pi} -\theta\right) \\& = \left|OM\right| \times \cos \left({\mathrm \pi} -\theta\right) \times \cos \left({\mathrm \pi} -\theta\right) \\& \overset{\left[a\right]}= {\cos ^2}\theta, \\ y &= -\left| {OP} \right|\sin \left({\mathrm \pi} -\theta\right) \\& = -\left|OM\right| \times \cos \left({\mathrm \pi} -\theta\right) \times \sin \left({\mathrm \pi} -\theta\right) \\& \overset{\left[a\right]}= \sin \theta \cos \theta ,\end{split} \]（推导中用到：[a]）
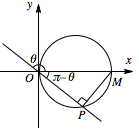当 $P$ 和 $O$，$M$ 点重合时，${\begin{cases}
x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}} $（$\theta $ 为参数）也成立．
所以 圆 ${x^2} + {y^2} - x = 0$ 的参数方程为：${\begin{cases}
x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}} $（$\theta $ 为参数）．
当 $P$ 在 $x$ 轴上方时，\[\begin{split} x &= \left| {OP} \right|\cos \theta \\& = \left|OM\right| \times \cos \theta \times \cos \theta \\& = {\cos ^2}\theta, \\ y &= \left| {OP} \right|\sin \theta \\& = \left|OM\right| \times \cos \theta \times \sin \theta \\& = \sin \theta \cos \theta ,\end{split} \]
当 $P$ 在 $x$ 轴下方时，\[\begin{split} x &= \left| {OP} \right|\cos \left({\mathrm \pi} -\theta\right) \\& = \left|OM\right| \times \cos \left({\mathrm \pi} -\theta\right) \times \cos \left({\mathrm \pi} -\theta\right) \\& \overset{\left[a\right]}= {\cos ^2}\theta, \\ y &= -\left| {OP} \right|\sin \left({\mathrm \pi} -\theta\right) \\& = -\left|OM\right| \times \cos \left({\mathrm \pi} -\theta\right) \times \sin \left({\mathrm \pi} -\theta\right) \\& \overset{\left[a\right]}= \sin \theta \cos \theta ,\end{split} \]（推导中用到：[a]） 当 $P$ 和 $O$，$M$ 点重合时，${\begin{cases}x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}} $（$\theta $ 为参数）也成立．
所以 圆 ${x^2} + {y^2} - x = 0$ 的参数方程为：${\begin{cases}
x = {\cos ^2}\theta \\
y = \sin \theta \cos \theta \\
\end{cases}} $（$\theta $ 为参数）．
题目
答案
解析
备注
