在区间 $\left[ { - 3,3} \right]$ 上随机取一个数 $x$，使得 $\left| {x + 1} \right| - \left| {x - 2} \right| \geqslant 1$ 成立的概率为 ．
【难度】
【出处】
2013年高考山东卷（理）
【标注】
【答案】
$\dfrac 1 3 $
【解析】
本题是考查几何概型与解不等式的综合考查，但难点是解绝对值不等式．解绝对值不等式可以用零点分段法、绝对值的几何意义或平方等来解，此题用几何意义相对简单，计算量不大．由绝对值的几何意义可知，不等式 $\left| {x + 1} \right| - \left| {x - 2} \right| \geqslant 1$ 的解集是数轴上到 $-1$ 的距离与到 $2$ 的距离的差大于等于 $1$ 的点的集合，如图所示：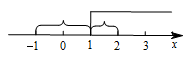
所以在 $\left[-3,3\right]$ 区间中能使不等式成立的 $x$ 的集合为 $\left[1,3\right]$，因此概率为 $P=\dfrac{2}{6}=\dfrac{1}{3}$．
所以在 $\left[-3,3\right]$ 区间中能使不等式成立的 $x$ 的集合为 $\left[1,3\right]$，因此概率为 $P=\dfrac{2}{6}=\dfrac{1}{3}$．
题目
答案
解析
备注
