给定区域 $D:{\begin{cases}
x + 4y \geqslant 4, \\
x + y \leqslant 4, \\
x \geqslant 0, \\
\end{cases}}$ 令点集\[T = \left\{ {\left( {{x_0},{y_0}} \right) \in D\left|\right.{x_0},{y_0} \in {\mathbb{Z}}} \right. ,\left( {{x_0},{y_0}} \right) 是 z = x + y 在 D 上取得最大值或最小值的 点 \left.\right\} ,\]则 $T$ 中的点共确定 条不同的直线．
x + 4y \geqslant 4, \\
x + y \leqslant 4, \\
x \geqslant 0, \\
\end{cases}}$ 令点集\[T = \left\{ {\left( {{x_0},{y_0}} \right) \in D\left|\right.{x_0},{y_0} \in {\mathbb{Z}}} \right. ,\left( {{x_0},{y_0}} \right) 是 z = x + y 在 D 上取得最大值或最小值的 点 \left.\right\} ,\]则 $T$ 中的点共确定
【难度】
【出处】
2013年高考广东卷（理）
【标注】
【答案】
$ 6 $
【解析】
解决此题的关键是写出 $T$ 中元素，集合 $T$ 中的元素是目标函数 $z=x+y$ 取得最大值或最小值得整数点，因此利用线性规划的知识将 $T$ 中的元素一一写出，两点确定一条直线，即可解决此题．不等式组所表示的平面区域如图阴影部分所示：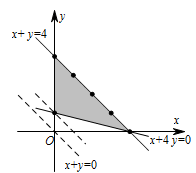
因为直线 $ z=x+y $ 与直线 $ x+y=4 $ 平行，故直线 $ z=x+y $ 过直线 $ x+y=4 $ 上的整数点 $ \left(4,0\right),\left(3,1\right),\left(2,2\right),\left(1,3\right),\left(0,4\right) $ 时，直线的纵截距最大，即 $ z $ 最大．
当直线过 $ \left(0,1\right) $ 时，直线的纵截距最小，即 $ z $ 最小，从而点集 $ T=\left\{\left(4,0\right),\left(3,1\right),\left(2,2\right),\left(1,3\right),\left(0,4\right),\left(0,1\right)\right\}$，经过这六个点的直线一共有 $ 6 $ 条．即 $ T $ 中的点共确定 $ 6 $ 条不同的直线．
因为直线 $ z=x+y $ 与直线 $ x+y=4 $ 平行，故直线 $ z=x+y $ 过直线 $ x+y=4 $ 上的整数点 $ \left(4,0\right),\left(3,1\right),\left(2,2\right),\left(1,3\right),\left(0,4\right) $ 时，直线的纵截距最大，即 $ z $ 最大．当直线过 $ \left(0,1\right) $ 时，直线的纵截距最小，即 $ z $ 最小，从而点集 $ T=\left\{\left(4,0\right),\left(3,1\right),\left(2,2\right),\left(1,3\right),\left(0,4\right),\left(0,1\right)\right\}$，经过这六个点的直线一共有 $ 6 $ 条．即 $ T $ 中的点共确定 $ 6 $ 条不同的直线．
题目
答案
解析
备注
