如图,$AB$ 是圆 $O$ 的直径,点 $C$ 在圆 $O$ 上,延长 $BC$ 到 $D$ 使 $BC = CD$,过 $C$ 作圆 $O$ 的切线交 $AD$ 于 $E$.若 $AB = 6$,$ED = 2$,则 $BC = $ .

【难度】
【出处】
2013年高考广东卷(理)
【标注】
【答案】
$2\sqrt{3}$
【解析】
本题考查的是相似三角形,属于基础题.联结 $OC$,因为 $O$ 是 $BA$ 的中点,$C$ 为 $BD$ 的中点,所以 $OC\parallel AD$.因为 $CE$ 为圆 $O$ 的切线,所以 $OC\perp CE$,所以 $AD\perp CE$,故 $\angle CED=90^\circ$.因为 $AC$ 垂直且平分 $BD$,所以 $AB=AD$,于是 $\angle ABC=\angle ADC$,所以 $\triangle ABC\sim \triangle CDE$,所以 $CD\cdot BC=AB\cdot ED$,因此 $BC=2\sqrt 3$.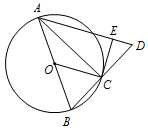

题目
答案
解析
备注