直线 $y = 4x$ 与曲线 $y = {x^3}$ 在第一象限内围成的封闭图形的面积为 \((\qquad)\)
【难度】
【出处】
2014年高考山东卷（理）
【标注】
【答案】
D
【解析】
本小题考查的是求定积分．直线 $y=4x$ 与曲线 $y=x^3$ 在第一象限内围成的封闭图形为图中阴影部分：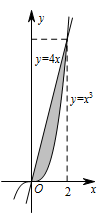
阴影部分的面积$S=\int_0^2\left(4x-x^3\right){\mathrm d}x=\left.\left(2x^2-\dfrac{1}{4}x^4\right)\right|_0^2=4$．
阴影部分的面积$S=\int_0^2\left(4x-x^3\right){\mathrm d}x=\left.\left(2x^2-\dfrac{1}{4}x^4\right)\right|_0^2=4$．
题目
答案
解析
备注
