查看数据源：599165c02bfec200011dfd0a
已知函数 $f\left(x\right) = |x - 2| + 1$，$g\left(x\right) = kx$，若方程 $f\left(x\right) = g\left(x\right)$ 有两个不相等的实根，则实数 $k$ 的取值范围是 \((\qquad)\)
A: $\left(0,\dfrac{1}{2}\right)$
B: $\left(\dfrac{1}{2},1\right)$
C: $\left(1,2\right)$
D: $\left(2, + \infty \right)$
【难度】
【出处】
2014年高考山东卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    绝对值函数
  • 知识点
    >
    函数
    >
    函数的图象与性质
  • 题型
    >
    函数
【答案】
B
【解析】
本题考查的两个函数的交点问题，两个函数的图象相对比较简单，且动直线过原点，故可以通过数形结合的方法求得斜率的取值范围．方程 $f\left(x\right)=g\left(x\right)$ 有两个不相等的实根，即曲线 $f\left(x\right)=|x-2|+1$ 与直线 $g\left(x\right)=kx$ 有两个不同的交点，函数 $f\left(x\right) = |x - 2| + 1$ 的图象如图所示．由图可知，当 $\dfrac{1}{2}<k<1$ 时，直线与曲线有两个交点，故当 $ k $ 的范围为 $ \left(\dfrac{1}{2},1\right) $，$f\left(x\right) = g\left(x\right)$ 有两个不相等的实根，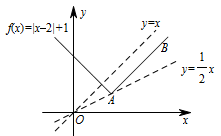
题目 答案 解析 备注
0.106985s