若 $x,y$ 满足 $\begin{cases}
x + y - 2 \geqslant 0 ,\\
kx - y + 2 \geqslant 0 ,\\
y \geqslant 0 ,\\
\end{cases}$ 且 $z = y - x$ 的最小值为 $ - 4$，则 $k$ 的值为 \((\qquad)\)
x + y - 2 \geqslant 0 ,\\
kx - y + 2 \geqslant 0 ,\\
y \geqslant 0 ,\\
\end{cases}$ 且 $z = y - x$ 的最小值为 $ - 4$，则 $k$ 的值为 \((\qquad)\)
【难度】
【出处】
2014年高考北京卷（理）
【标注】
【答案】
D
【解析】
本题考查线性规划的相关知识，注意参数对直线位置的影响．当 $k \geqslant 0$ 时，$z = y - x$ 没有最小值，不合题意，故 $k<0$，此时不等式组所表示的平面区域如图所示：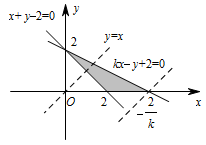
由图可知，$z = y - x$ 在点 $\left( { - \dfrac{2}{k},0} \right)$ 处取最小值．
故 $0 - \left( { - \dfrac{2}{k}} \right) = - 4$，解得 $k = - \dfrac{1}{2}$．
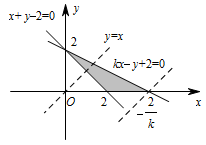由图可知，$z = y - x$ 在点 $\left( { - \dfrac{2}{k},0} \right)$ 处取最小值．故 $0 - \left( { - \dfrac{2}{k}} \right) = - 4$，解得 $k = - \dfrac{1}{2}$．
题目
答案
解析
备注
