查看数据源：599165bf2bfec200011dfc49
在空间直角坐标系 $O-xyz$ 中，已知 $A\left( {2,0,0} \right) $，$B\left( {2,2,0} \right)$，$ C\left( {0,2,0} \right) $，$ D\left(1,1,\sqrt 2 \right)$．若 ${S_1}$，${S_2}$，${S_3}$ 分别表示三棱锥 $D - ABC$ 在 $xOy$，$yOz$，$zOx$ 坐标平面上的正投影图形的面积，则 \((\qquad)\)
A: ${S_1} = {S_2} = {S_3}$
B: ${S_2} = {S_1} 且 {S_2} \ne {S_3}$
C: ${S_3} = {S_1} 且 {S_3} \ne {S_2}$
D: ${S_3} = {S_2} 且 {S_3} \ne {S_1}$
【难度】
【出处】
2014年高考北京卷（理）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    多面体
    >
    棱锥
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的投影
  • 题型
    >
    立体几何
【答案】
D
【解析】
本题考查三棱锥的三视图相关问题．分别将个点在各个面上的投影对应的点坐标写出，计算面积即可．设 $ D $ 在空间直角坐标系$O-xyz$ 中 $xOy $、$yOz$ 和 $zOx$ 平面上的正投影分别为 $D_1 $、${D_2}$ 和 ${D_3}$，如图所示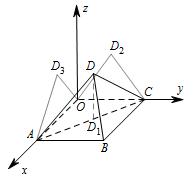：则 $D_1\left(1,1,0\right) $，${D_2}\left( {0,1,\sqrt 2 } \right) $，$ {D_3}\left( {1,0,\sqrt 2 } \right)$．
三棱锥 $D - ABC$ 在平面 $xOy $、$yOz$ 和 $zOx$ 上的投影分别为 $\triangle ABC$、$\triangle OC{D_2}$ 和 $\triangle OA{D_3}$．
故 ${S_1} = 2$，${S_2} = {S_3} = \sqrt 2 $．
题目 答案 解析 备注
0.122177s