查看数据源：599165c72bfec200011e1212
函数 $y = f\left(x\right)$ 的图象如图所示，在区间 $\left[ {a,b} \right]$ 上可找到 $n\left(n \geqslant 2\right)$ 个不同的数 ${x_1},{x_2}, \cdots ,{x_n}$，使得 $\dfrac{{f\left({x_1}\right)}}{x_1} = \dfrac{{f\left({x_2}\right)}}{x_2} = \cdots = \dfrac{{f\left({x_n}\right)}}{x_n}$，则 $n$ 的取值范围为 \((\qquad)\)  
A: $\left\{ {2,3} \right\}$
B: $\left\{ {2,3,4} \right\}$
C: $\left\{ {3,4} \right\}$
D: $\left\{ {3,4,5} \right\}$
【难度】
【出处】
2013年高考安徽卷（文）
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
  • 方法
    >
    数形结合
  • 题型
    >
    函数
【答案】
B
【解析】
可以转化为过原点的直线与函数图象交点的个数问题来解答．令 $\dfrac{f\left(x\right)}{x}=m$，则可将所求转化为直线 $y=mx$ 与曲线 $y=f\left(x\right)$ 的交点个数问题并利用数形结合求解．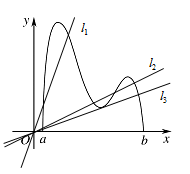 
题目 答案 解析 备注
0.137926s