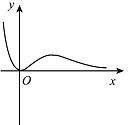
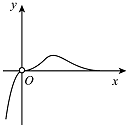
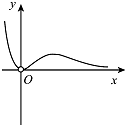
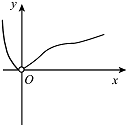
函数 $y = \dfrac{x^3}{{{3^x} - 1}}$ 的图象大致是 \((\qquad)\)
【难度】
【出处】
2013年高考四川卷(理)
【标注】
【答案】
C
【解析】
先看定义域,再看自变量对应函数值的符号,最后看看单调性的情况即可完成该题的解答.根据函数的定义域,知 $\left\{x|x \in \mathbb R,x\neq 0\right\} $,所以 A 不正确;当 $ x <0 $ 时,函数 $y=x^3 $ 小于 $0 $,函数 $y=3^x-1 $ 小于 $0 $,故当 $ x < 0 $ 时,函数 $y = \dfrac{x^3}{{{3^x} - 1}}$ 大于 $ 0 $.所以 B 不正确;因为 $ x =1 $ 时,$y= \dfrac 12 $,$ x =2 $ 时,$y=1 $,$ x =4 $ 时,$y= \dfrac 45 $,所以当 $ x>0 $ 时,函数 $y$ 不单调,所以 D 不正确.函数 $y = \dfrac{x^3}{{{3^x} - 1}}$ 的图象大致是 C 所示的图象.
题目
答案
解析
备注