在平面直角坐标系 $xOy$ 中,点 $P$ 的坐标为 $(3,4)$,点 $Q$ 在 $x$ 轴的正半轴上,点 $R$ 在 $y$ 轴的正半轴上.若 $\triangle PQR$ 是等边三角形,则其边长等于 .
【难度】
【出处】
全国高中数学联赛模拟试题(3)
【标注】
【答案】
$2\sqrt{25-12\sqrt{3}}$
【解析】
如图所示,设 $\triangle PQR$ 的边长 $a$.过点 $P$ 作 $PE\perp x$ 轴,垂足为 $E$,$PF\perp y$ 轴,垂足为 $F$.设 $\angle RPF=\theta$,则 $\angle RPE=90^{\circ}-\theta, \angle QPE=60^{\circ}-\angle RPE=\theta-30^{\circ}$,所以$$\left\{\begin{aligned}
&a\cos\theta=3,\\
&a\cos(\theta-30^{\circ})=4.\\
\end{aligned}\right.$$于是$$a\cos\theta\cos 30^{\circ}+a\sin\theta\sin 30^{\circ}=4\Rightarrow 3\cdot \frac{\sqrt{3}}{2}+a\sin\theta \cdot \frac{1}{2}=4,$$即 $a\sin\theta=8-3\sqrt{3}$.所以$$a^2=(a\cos\theta)^2+(a\sin\theta)^2=3^2+(8-3\sqrt{3})^2=100-48\sqrt{3},$$故 $a=\sqrt{100-48\sqrt{3}}=2\sqrt{25-12\sqrt{3}}$.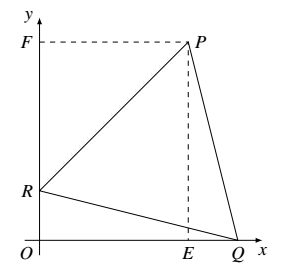
&a\cos\theta=3,\\
&a\cos(\theta-30^{\circ})=4.\\
\end{aligned}\right.$$于是$$a\cos\theta\cos 30^{\circ}+a\sin\theta\sin 30^{\circ}=4\Rightarrow 3\cdot \frac{\sqrt{3}}{2}+a\sin\theta \cdot \frac{1}{2}=4,$$即 $a\sin\theta=8-3\sqrt{3}$.所以$$a^2=(a\cos\theta)^2+(a\sin\theta)^2=3^2+(8-3\sqrt{3})^2=100-48\sqrt{3},$$故 $a=\sqrt{100-48\sqrt{3}}=2\sqrt{25-12\sqrt{3}}$.

题目
答案
解析
备注