已知平面上两个点集$$M=\{(x,y)~|~|x+y+1|\geqslant \sqrt{2(x^2+y^2)}, x,y\in\mathbb{R}\}$$$$N=\{(x,y)~|~|x-a|+|y-1|\leqslant 1, x,y\in\mathbb{R}\}.$$若 $M\cap N\neq \emptyset$，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
全国高中数学联赛模拟试题(4)
【标注】
【答案】
$[1-\sqrt{6},3+\sqrt{10}]$
【解析】
由题意知，$M$ 是以坐标原点为焦点，直线 $x+y+1=0$ 为准线的抛物线上及其凹口内侧的点集，$N$ 是以 $(a,1)$ 为中心的正方形及其内部的点集，如图所示．
下面考察 $M\cap N=\emptyset$ 时，$a$ 的取值范围．
令 $y=1$，代入方程 $|x+y+1|=\sqrt{2(x^2+y^2)}$，得 $x^2-4x-2=0$．解得 $x=2\pm\sqrt{6}$．所以当 $a<2-\sqrt{6}-1=1-\sqrt{6}$ 时，$M\cap N=\emptyset$．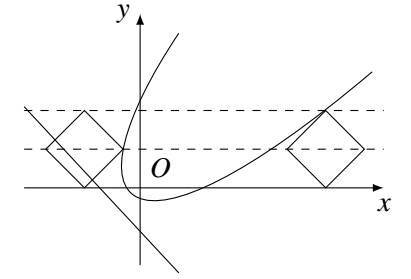
令 $y=2$，代入方程 $|x+y+1|=\sqrt{2(x^2+y^2)}$，得 $x^2-6x-1=0$．解得 $x=3\pm \sqrt{10}$．所以当 $a>3+\sqrt{10}$ 时，$M\cap N=\emptyset$．
从而，当 $1-\sqrt{6}\leqslant a\leqslant 3+\sqrt{10}$ 时，$M\cap N\neq \emptyset$．
下面考察 $M\cap N=\emptyset$ 时，$a$ 的取值范围．
令 $y=1$，代入方程 $|x+y+1|=\sqrt{2(x^2+y^2)}$，得 $x^2-4x-2=0$．解得 $x=2\pm\sqrt{6}$．所以当 $a<2-\sqrt{6}-1=1-\sqrt{6}$ 时，$M\cap N=\emptyset$．
令 $y=2$，代入方程 $|x+y+1|=\sqrt{2(x^2+y^2)}$，得 $x^2-6x-1=0$．解得 $x=3\pm \sqrt{10}$．所以当 $a>3+\sqrt{10}$ 时，$M\cap N=\emptyset$．从而，当 $1-\sqrt{6}\leqslant a\leqslant 3+\sqrt{10}$ 时，$M\cap N\neq \emptyset$．
题目
答案
解析
备注
