查看数据源：59a52d7e9ace9f000124d006
函数 $f\left( x \right) = 2\ln x$ 的图象与函数 $g\left( x \right) = {x^2} - 4x + 5$ 的图象的交点个数为 \((\qquad)\)
A: $ 3 $
B: $ 2 $
C: $ 1 $
D: $ 0 $
【难度】
【出处】
2013年高考湖南卷（理）
【标注】
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    对数函数
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    二次函数
  • 题型
    >
    函数
【答案】
B
【解析】
本题考查二次函数和对数函数的图象与性质，注意二次函数最小值点位于对数函数图象下方．根据对数函数与二次函数的性质，画出图象如图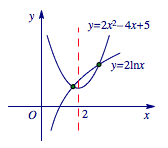， 当 $x=2 $ 时，$f\left( 2 \right) = 2\ln 2 = \ln 4 $，所以 $f\left(2\right)> 1 = g\left( 2 \right)$，则点 $\left(2,2\ln 2\right) $ 在点 $\left(2,1\right) $ 的上方．因此，交点共有两个．
题目 答案 解析 备注
0.115054s