在等腰直角三角形 $ABC$ 中，$AB=AC = 4$，点 $P$ 是边 $AB$ 上异于 $A,B$ 的一点，光线从点 $P$ 出发，经 $BC,CA$ 反射后又回到点 $P$（如图）．若光线 $QR$ 经过 $\triangle ABC$ 的重心，则 $AP$ 等于 \((\qquad)\) 
【难度】
【出处】
2013年高考湖南卷（理）
【标注】
【答案】
D
【解析】
光路传播问题，可以引入坐标系进行求解，注意反射问题一般做对称求解．如图，以 $ A$ 为原点，$ AB$ 所在直线为 $x $ 轴，建立平面直角坐标系．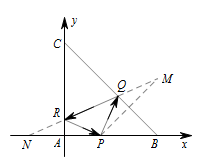
易知 $B\left( {4,0} \right),C\left( {0,4} \right)$，从而直线 $BC $ 的方程为\[x + y = 4,\]$\triangle ABC $ 的重心为\[G\left( {\dfrac{4}{3},\dfrac{4}{3}} \right).\]设 $P\left(t,0\right) $ 为线段 $ AB$ 上一点，则 $P $ 关于直线 $AC,BC$ 的对称点分别为\[ N\left(-t,0\right), M\left(4,4-t\right),\]所以直线 $ MN$ 的方程为\[y = \dfrac{4 - t}{4 + t}\left( {x+ t} \right).\]根据题意，$G$ 在直线 $ MN$ 上，则\[\dfrac{4}{3} = \dfrac{4 - t}{4 + t}\left( {\dfrac{4}{3} + t} \right),\]解得 $t=\dfrac 43 $．
易知 $B\left( {4,0} \right),C\left( {0,4} \right)$，从而直线 $BC $ 的方程为\[x + y = 4,\]$\triangle ABC $ 的重心为\[G\left( {\dfrac{4}{3},\dfrac{4}{3}} \right).\]设 $P\left(t,0\right) $ 为线段 $ AB$ 上一点，则 $P $ 关于直线 $AC,BC$ 的对称点分别为\[ N\left(-t,0\right), M\left(4,4-t\right),\]所以直线 $ MN$ 的方程为\[y = \dfrac{4 - t}{4 + t}\left( {x+ t} \right).\]根据题意，$G$ 在直线 $ MN$ 上，则\[\dfrac{4}{3} = \dfrac{4 - t}{4 + t}\left( {\dfrac{4}{3} + t} \right),\]解得 $t=\dfrac 43 $．
题目
答案
解析
备注
