已知椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（$a>b>0$）的上顶点为 $A$，直线 $y=x-3$ 与椭圆交于 $P,Q$ 两点．若 $\triangle APQ$ 的重心是椭圆的右焦点，则椭圆的右焦点坐标是 ．
【难度】
【出处】
全国高中数学联赛模拟试题(10)
【标注】
【答案】
$\left(\frac{27-3\sqrt{5}}{19},0\right)$
【解析】
如图所示，设 $P$ 的坐标是 $(x_1,y_1)$，$Q$ 的坐标是 $(x_2,y_2)$，椭圆的右焦点 $F$ 的坐标为 $(c,0)$，则由 $\triangle APQ$ 的重心公式，有$$c=\frac{x_1+x_2}{3}, 0=\frac{y_1+y_2+b}{3}.$$从而$$x_1+x_2=3c, y_1+y_2=-b.~~~~~ ① $$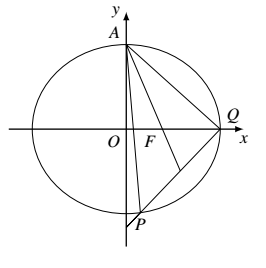
将 $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1, \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 相减得$$\frac{(x_1-x_2)(x_1+x_2)}{a^2}+\frac{(y_1-y_2)(y_1+y_2)}{b^2}=0.$$又 $\frac{y_1-y_2}{x_1-x_2}=1$，则$$\frac{x_1+x_2}{a^2}+\frac{y_1+y_2}{b^2}=0\Rightarrow \frac{3c}{a^2}+\frac{-b}{b^2}=0,$$即$$a^2=3bc.~~~~~~ ② $$由式 ① 知 $PQ$ 的中点 $M$ 的坐标为 $\left(\frac{3c}{2},-\frac{b}{2}\right)$，因为点 $M$ 在直线 $PQ$ 上，所以$$-\frac{b}{2}=\frac{3c}{2}-3\Rightarrow b+3c=6.~~~~ ③ $$由 $a^2=b^2+c^2$ 及式 ②，③ 消去 $a,b$，得$$(6-3c)^2+c^2=3(6-3c)c\Rightarrow 19c^2-54c+36=0.$$解得 $c=\frac{27\pm 3\sqrt{5}}{19}$．当 $c=\frac{27+3\sqrt{5}}{19}$ 时，经验证可知直线 $y=x-3$ 与椭圆没有交点，故 $\frac{27-3\sqrt{5}}{19}$．
因此，椭圆的右焦点的坐标为 $\left(\frac{27-3\sqrt{5}}{19},0\right)$．
将 $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1, \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 相减得$$\frac{(x_1-x_2)(x_1+x_2)}{a^2}+\frac{(y_1-y_2)(y_1+y_2)}{b^2}=0.$$又 $\frac{y_1-y_2}{x_1-x_2}=1$，则$$\frac{x_1+x_2}{a^2}+\frac{y_1+y_2}{b^2}=0\Rightarrow \frac{3c}{a^2}+\frac{-b}{b^2}=0,$$即$$a^2=3bc.~~~~~~ ② $$由式 ① 知 $PQ$ 的中点 $M$ 的坐标为 $\left(\frac{3c}{2},-\frac{b}{2}\right)$，因为点 $M$ 在直线 $PQ$ 上，所以$$-\frac{b}{2}=\frac{3c}{2}-3\Rightarrow b+3c=6.~~~~ ③ $$由 $a^2=b^2+c^2$ 及式 ②，③ 消去 $a,b$，得$$(6-3c)^2+c^2=3(6-3c)c\Rightarrow 19c^2-54c+36=0.$$解得 $c=\frac{27\pm 3\sqrt{5}}{19}$．当 $c=\frac{27+3\sqrt{5}}{19}$ 时，经验证可知直线 $y=x-3$ 与椭圆没有交点，故 $\frac{27-3\sqrt{5}}{19}$．因此，椭圆的右焦点的坐标为 $\left(\frac{27-3\sqrt{5}}{19},0\right)$．
题目
答案
解析
备注
