查看数据源：6254eec8ea59ab000a73e407
如图，在四棱锥 $S-ABCD$ 中，$\bigtriangleup ABS$ 是正三角形，四边形 $ABCD$ 是菱形，$AB=4, \angle ABC=120^\circ$，点 $E$ 是 $BS$ 的中点．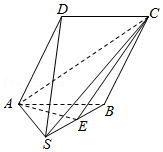
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    空间的平行关系
    >
    线面平行
  • 知识点
    >
    立体几何
    >
    空间几何量
    >
    空间的距离
    >
    点面距离
  1. 求证：$SD\parallel$ 平面 $ACE$；
    标注
    • 知识点
      >
      立体几何
      >
      空间位置关系
      >
      空间的平行关系
      >
      线面平行
    答案
    略
    解析
    略
  2. 若平面 $ABS\perp$ 平面 $ABCD$，求点 $E$ 到平面 $ASD$ 的距离．
    标注
    • 知识点
      >
      立体几何
      >
      空间几何量
      >
      空间的距离
      >
      点面距离
    答案
    即点 $E$ 到平面 $ASD$ 的距离为 $ \dfrac{\sqrt{15}}{5}$
    解析
    略
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.109947s