如图，已知平面四边形 $ABCD$，$AB=BC=3$，$CD=1$，$AD=\sqrt 5$，$\angle ADC=90^\circ $．沿直线 $AC$ 将 $\triangle ACD$ 翻折成 $\triangle ACD'$，直线 $AC$ 与 $BD'$ 所成角的余弦的最大值是 $\frac{\sqrt{b}}{a}$，其中 $a,b$ 是正整数且 $b$ 不含平方因子，则 $ab=$ ．
【难度】
【出处】
2016年高考浙江卷（文）
【标注】
【答案】
$36$
【解析】
如图，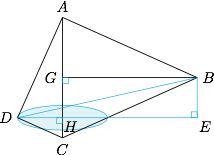
设直线 $AC$ 与 $BD'$ 所成角为 $\theta$，则$$\begin{split}\cos\theta&=\dfrac{\big|\overrightarrow{BD'}\cdot \overrightarrow{HG}\big|}{BD'\cdot HG}\\ &=\dfrac{\big|(\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})\cdot \overrightarrow{HG}\big|}{BD'\cdot HG}\\ &=\dfrac{GH^2}{BD'\cdot GH}\\ &=\dfrac{GH}{BD'},\end{split}$$而$$\begin{split}BD'&=\sqrt{(\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})\cdot (\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})}\\ &=\sqrt{BG^2+GH^2+HD'^2+2\overrightarrow{BG}\cdot\overrightarrow{HD'}},\end{split}$$于是 $BD'$ 的最小值为 $\sqrt{BG^2+GH^2+HD'^2-2BG\cdot HD'}$，进一步可以计算得所求的最大值为 $\dfrac{\sqrt 6}6$．
设直线 $AC$ 与 $BD'$ 所成角为 $\theta$，则$$\begin{split}\cos\theta&=\dfrac{\big|\overrightarrow{BD'}\cdot \overrightarrow{HG}\big|}{BD'\cdot HG}\\ &=\dfrac{\big|(\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})\cdot \overrightarrow{HG}\big|}{BD'\cdot HG}\\ &=\dfrac{GH^2}{BD'\cdot GH}\\ &=\dfrac{GH}{BD'},\end{split}$$而$$\begin{split}BD'&=\sqrt{(\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})\cdot (\overrightarrow{BG}+\overrightarrow{GH}+\overrightarrow{HD'})}\\ &=\sqrt{BG^2+GH^2+HD'^2+2\overrightarrow{BG}\cdot\overrightarrow{HD'}},\end{split}$$于是 $BD'$ 的最小值为 $\sqrt{BG^2+GH^2+HD'^2-2BG\cdot HD'}$，进一步可以计算得所求的最大值为 $\dfrac{\sqrt 6}6$．
题目
答案
解析
备注
