如图(1),在矩形 $ABCD$ 中,$AB=6, AD=4, E, F$ 分别为 $BC, AD$ 的中点,将矩形 $ABCD$ 沿着 $EF$ 折叠,使 $\angle AFD=60^\circ$,如图(2),$G$ 为 $AF$ 的中点.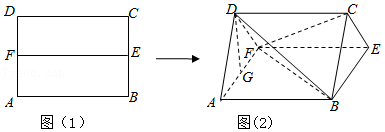

【难度】
【出处】
无
【标注】
-
(Ⅰ)求证:$DG\perp BF$;标注答案略解析略
-
(Ⅱ)求点 $D$ 到平面 $BCF$ 的距离.标注答案$ h=\dfrac{6}{13} \sqrt{13}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2