若平面向量 $\overrightarrow a,\overrightarrow b$ 满足 $\overrightarrow a\cdot \overrightarrow a=1$，$\overrightarrow b\cdot \overrightarrow b=4$，$\overrightarrow a\cdot \overrightarrow b=1$，$\overrightarrow e$ 是平面内的单位向量，$\Big|\overrightarrow a\cdot \overrightarrow e\Big|+\Big|\overrightarrow b\cdot \overrightarrow e\Big|$ 的取值范围是 $[m, M]$，则 $M^2+8m^2=$ ．
【难度】
【出处】
无
【标注】
【答案】
$13$
【解析】
设 $\overrightarrow a=(1,0)$，$\overrightarrow b=\left(1,\sqrt 3\right)$，$\overrightarrow e=\left(\cos \theta,\sin\theta\right)$，则\[\begin{split} \left|\overrightarrow a\cdot \overrightarrow e\right|+\left|\overrightarrow b\cdot \overrightarrow e\right|&=\left|\cos\theta\right|+\left|\cos\theta+\sqrt 3\sin\theta\right|\\
&=\begin{cases} \left|2\cos\theta+\sqrt 3\sin\theta\right|,&\theta\in\left(-\dfrac{\pi}6+k\pi,\dfrac{\pi}2+k\pi\right],\\ \left|\sqrt 3\sin\theta\right|,&\theta\in\left(\dfrac {\pi}2,\dfrac{5\pi}6+k\pi\right],\end{cases} \end{split}\]其中 $k\in\mathbb Z$．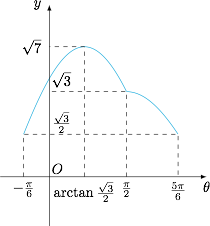
如图，函数值域即所求的取值范围，为 $\left[\dfrac{\sqrt 3}2,\sqrt 7\right]$．
&=\begin{cases} \left|2\cos\theta+\sqrt 3\sin\theta\right|,&\theta\in\left(-\dfrac{\pi}6+k\pi,\dfrac{\pi}2+k\pi\right],\\ \left|\sqrt 3\sin\theta\right|,&\theta\in\left(\dfrac {\pi}2,\dfrac{5\pi}6+k\pi\right],\end{cases} \end{split}\]其中 $k\in\mathbb Z$．
如图，函数值域即所求的取值范围，为 $\left[\dfrac{\sqrt 3}2,\sqrt 7\right]$．
题目
答案
解析
备注
