已知点 $A(1,-1)$，$B(4,0)$，$C(2,2)$．平面区域 $D$ 是由所有满足 $\overrightarrow {AP}=\lambda\overrightarrow {AB} +\mu \overrightarrow {AC}(1<\lambda \leqslant a,1<\mu \leqslant b)$ 的点 $P(x,y)$ 组成的区域．若区域 $D$ 的面积为 $8$，则 $a+b$ 的最小值为 ．
【难度】
【出处】
2014年全国高中数学联赛福建省预赛
【标注】
【答案】
$4$
【解析】
如图，延长 $AB$ 至点 $N$，延长 $AC$ 至点 $M$，使得$$|AN|=a|AB| , |AM|=b|AC|.$$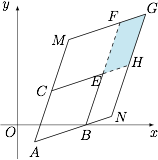
四边形 $ABEC$，$ANGM$，$EHGF$ 均为平行四边形．
由条件知，点 $P(x,y)$ 组成的区域 $D$ 为图中的阴影部分，即四边形 $EHGF$（不含边界 $EH$，$EF$）．
因为 $\overrightarrow {AB}=(3,1)$，$\overrightarrow {AC}=(1,3)$，$\overrightarrow {BC}=(-2,2)$，所以$$|AB|=\sqrt {10},|AC|=\sqrt {10},|BC|=2\sqrt {2},$$且$$\cos \angle CAB=\dfrac {10+10-8}{2\times \sqrt {10}\times \sqrt {10}}=\dfrac 35 , \sin \angle CAB=\dfrac 45,$$故四边形 $EHGF$ 的面积为$$(a-1)\sqrt {10}\times (b-1)\sqrt {10}\times \dfrac 45=8,$$所以$$(a-1)(b-1)=1,$$因此$$a+b=a+\left(\dfrac {1}{a-1}+1\right)=(a-1)+\dfrac {1}{a-1}+2\leqslant 4,$$由 $a>1$，$b>1$ 知，当且仅当 $a-1=1$，即 $a=b=2$ 时，$a+b$ 取最小值 $4$．
四边形 $ABEC$，$ANGM$，$EHGF$ 均为平行四边形．由条件知，点 $P(x,y)$ 组成的区域 $D$ 为图中的阴影部分，即四边形 $EHGF$（不含边界 $EH$，$EF$）．
因为 $\overrightarrow {AB}=(3,1)$，$\overrightarrow {AC}=(1,3)$，$\overrightarrow {BC}=(-2,2)$，所以$$|AB|=\sqrt {10},|AC|=\sqrt {10},|BC|=2\sqrt {2},$$且$$\cos \angle CAB=\dfrac {10+10-8}{2\times \sqrt {10}\times \sqrt {10}}=\dfrac 35 , \sin \angle CAB=\dfrac 45,$$故四边形 $EHGF$ 的面积为$$(a-1)\sqrt {10}\times (b-1)\sqrt {10}\times \dfrac 45=8,$$所以$$(a-1)(b-1)=1,$$因此$$a+b=a+\left(\dfrac {1}{a-1}+1\right)=(a-1)+\dfrac {1}{a-1}+2\leqslant 4,$$由 $a>1$，$b>1$ 知，当且仅当 $a-1=1$，即 $a=b=2$ 时，$a+b$ 取最小值 $4$．
题目
答案
解析
备注
