抛物线 $y^2=2px(p>0)$ 的焦点为 $F$，准线为 $l$，$A,B$ 是抛物线上的两个动点，且满足 $\angle AFB=\dfrac{\pi}{3}$．设线段 $AB$ 的中点 $M$ 在 $l$ 上的投影为 $N$，则 $\dfrac{|MN|}{|AB|}$ 的最大值是 ．
【难度】
【出处】
2012年全国高中数学联赛（一试）
【标注】
【答案】
$1$
【解析】
如图，设 $FA=a$，$FB=b$．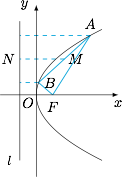
根据题意，有\[|MN|=\dfrac {a+b}2,\]在 $\triangle ABC$ 中应用余弦定理，有\[|AB|^2=a^2+b^2-ab,\]于是\[\begin{split}\dfrac{|MN|}{|AM|}&=\dfrac 12\sqrt{\dfrac{(a+b)^2}{a^2+b^2-ab}}\\
&=\dfrac 12\sqrt{1+\dfrac{3}{\dfrac ab+\dfrac ba-1}}\\
&\leqslant 1,\end{split}\]等号当且仅当 $a=b$，即 $A,B$ 关于 $x$ 轴对称时取得．因此所求的最大值为 $1$．
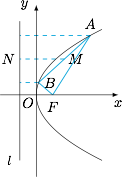根据题意，有\[|MN|=\dfrac {a+b}2,\]在 $\triangle ABC$ 中应用余弦定理，有\[|AB|^2=a^2+b^2-ab,\]于是\[\begin{split}\dfrac{|MN|}{|AM|}&=\dfrac 12\sqrt{\dfrac{(a+b)^2}{a^2+b^2-ab}}\\&=\dfrac 12\sqrt{1+\dfrac{3}{\dfrac ab+\dfrac ba-1}}\\
&\leqslant 1,\end{split}\]等号当且仅当 $a=b$，即 $A,B$ 关于 $x$ 轴对称时取得．因此所求的最大值为 $1$．
题目
答案
解析
备注
