如图,在三棱锥 $P-ABC$ 中,$\triangle PAC,\triangle ABC$ 都是边长为 $6$ 的等边三角形.若二面角 $P-AC-B$ 的大小为 $120^\circ$,则三棱锥 $P-ABC$ 的外接球的面积为 $\pi$.

【难度】
【出处】
2018年全国高中数学联赛福建省预赛
【标注】
【答案】
$84$
【解析】
如图,取 $AC$ 的中点 $D$,连结 $DP,DB$,则由 $\triangle PAC,\triangle ABC$ 都是边长为 $6$ 的等边三角形,得 $PD\bot AC,BD\bot AC,\angle PDB$ 为二面角 $P-AC-B$ 的平面角,$\angle PDB=120^\circ$.
设 $O$ 为三棱锥 $P-ABC$ 的外接球的球心,$O_1,O_2$ 分别为 $\triangle ABC,\triangle PAC$ 的中心.则 $OO_1\bot$ 面 $ABC$,$OO_2\bot$ 面 $PAC$,且 $O_2D=O_1D=\dfrac{1}{3}(\dfrac{\sqrt {3}}{2}\times 6)=\sqrt{3},OO_2=OO_1$.易知 $O_1,O_2,D,O_1$ 四点共面,连结 $OD$,则 $\angle ODO_1=60^\circ,OO_1=\sqrt{3}DO_1=3$.所以三棱锥 $P-ABC$ 的外接球半径 $R=OB=\sqrt{OO_1^2+O_1B^2}=\sqrt{3^2+(2\sqrt{3})^2}=\sqrt{21}$.所以三棱锥 $P-ABC$ 的外接球的面积为 $4\pi R^2=84\pi$.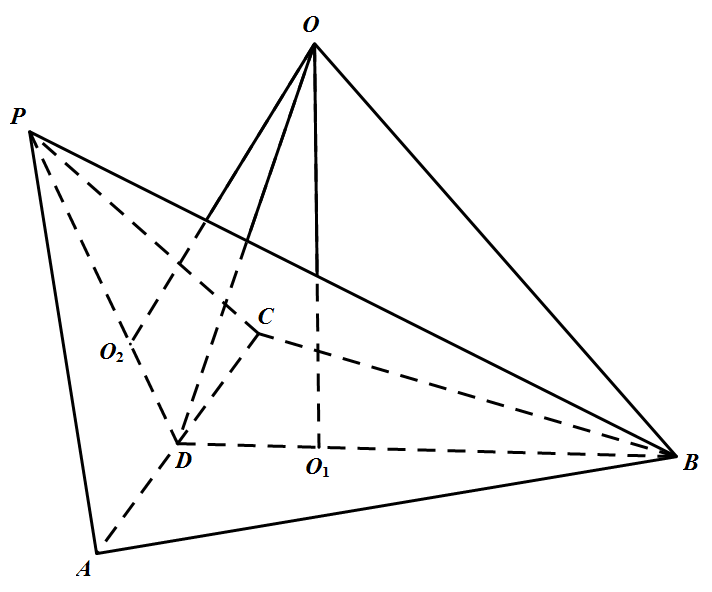
设 $O$ 为三棱锥 $P-ABC$ 的外接球的球心,$O_1,O_2$ 分别为 $\triangle ABC,\triangle PAC$ 的中心.则 $OO_1\bot$ 面 $ABC$,$OO_2\bot$ 面 $PAC$,且 $O_2D=O_1D=\dfrac{1}{3}(\dfrac{\sqrt {3}}{2}\times 6)=\sqrt{3},OO_2=OO_1$.易知 $O_1,O_2,D,O_1$ 四点共面,连结 $OD$,则 $\angle ODO_1=60^\circ,OO_1=\sqrt{3}DO_1=3$.所以三棱锥 $P-ABC$ 的外接球半径 $R=OB=\sqrt{OO_1^2+O_1B^2}=\sqrt{3^2+(2\sqrt{3})^2}=\sqrt{21}$.所以三棱锥 $P-ABC$ 的外接球的面积为 $4\pi R^2=84\pi$.

题目
答案
解析
备注