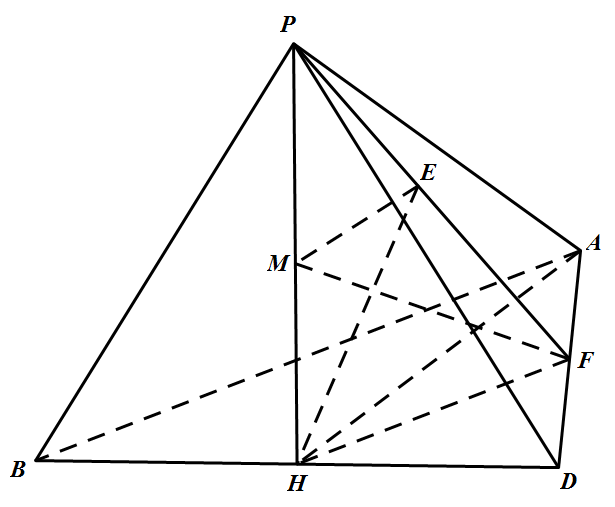设菱形两对角线 $AC,BD$ 的交点为 $H$，则 $PH$ 即是线段 $AC$ 的中垂线，又是 $BD$ 的中垂线，故是四棱锥的高，且点 $M$ 在 $PH$ 上，于是平面 $PBD$ 与底面 $ABCD$ 垂直，同理平面 $PAC$ 也与底面 $ABCD$ 垂直，平面 $PBD$ 将四棱锥分成两个等积的四面体．只需考虑四面体 $P-ABCD$．如图，设点 $M$ 在面 $PAD$ 上的投影为 $E$，平面 $MEH$ 过点 $P$，且交 $AD$ 于 $F$，因 $\angle MHF=90^\circ=\angle MEF$，则 $M,E,F,H$ 四点共圆．由于 $ME\bot$ 面 $PAD$，得 $ME\bot AD$，由 $MH\bot$ 面 $ABD$，得 $MH\bot AD$，所以 $AD\bot$ 面 $MEH$，故 $AD\bot PF$．$FH$ 是 $PF$ 在面 $ABD$ 内的射影，则 $AD\bot FH$，即二面角的平面角 $\angle EFH=60^\circ$，于是 $\angle EMH=120^\circ$．据 $ME=MH=1$，得 $EH=\sqrt{3}$，故直角三角形 $MEF$ 与 $MHF$ 中，$EF=HF$．因 $\angle EFH=60^\circ$，所以 $\triangle EFH$ 是正三角形，即 $FH=EF=H=\sqrt{3}$．在直角 $\triangle AFH$ 中，$\angle HAF=30^\circ$，则 $AH=2FH=\sqrt{3}$，故正 $\triangle ABD$ 的边长为 $4$，于是 $S_{\triangle ABD}=4\sqrt{3}$．在直角 $\triangle PFH$ 中，$PH=FH\tan 60^\circ=3,V_{P-ABD}=\dfrac{1}{3}PH\cdot S_{\triangle ABD}=4\sqrt{3}$，从而 $V_{P-ABCD}=2V_{P-ABD}=8\sqrt{3}$．