在 $\triangle ABC$ 中,已知 $AB=4,AC=3$.如图所示,$P$ 是边 $BC$ 的垂直平分线上一点,$\overrightarrow{BC}\cdot\overrightarrow{AP}=-\frac{p}{q}$,其中 $p,q$ 是互质的正整数,则 $p+q=$ .

【难度】
【出处】
2018年全国高中数学联赛甘肃省预赛
【标注】
【答案】
$9$
【解析】
如图所示,设 $Q$ 为 $BC$ 的中点,$\overrightarrow{BC}\cdot\overrightarrow{AP}=(\overrightarrow{AC}-\overrightarrow{AB})\cdot(\overrightarrow{AQ}+\overrightarrow{QP})=(\overrightarrow{AC}-\overrightarrow{AB})\cdot\overrightarrow{AQ}\\=(\overrightarrow{AC}-\overrightarrow{AB})\cdot\dfrac{1}{2}(\overrightarrow{AB}\cdot\overrightarrow{AC})=-\dfrac{7}{2}.$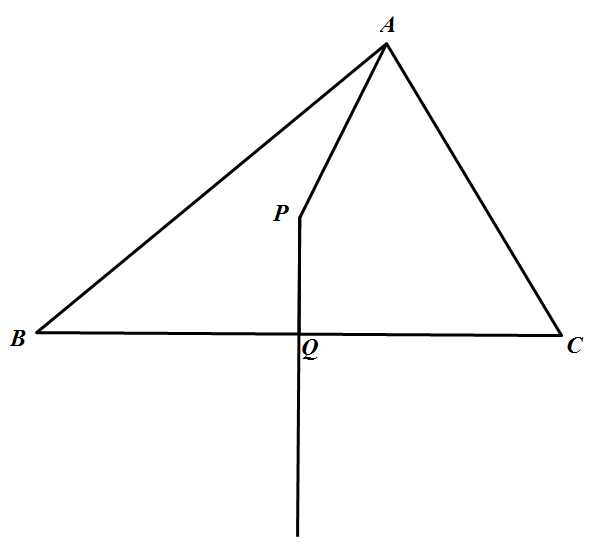

题目
答案
解析
备注