在 $\triangle ABC$ 中,$AB=5,AC=4$,且 $\overrightarrow{AB}\cdot\overrightarrow{AC}=12$.设 $P$ 为平面 $ABC$ 上的一点,$\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{PC})$ 的最小值是 $-\frac{a}{b}$,其中 $a,b$ 是互质的正整数.则 $a+b=$ .
【难度】
【出处】
2018年全国高中数学联赛江苏省预赛(初赛试题)
【标注】
【答案】
$73$
【解析】
由 $AB=5,AC=4$,且 $\overrightarrow{AB}\cdot\overrightarrow{AC}=12$ 得 $\cos A=\dfrac{3}{5}$.如图,以 $A$ 为坐标原点,$AC$ 为 $x$ 轴建立直角坐标系,则 $C(4,0),B(3,4)$.设 $P(x,y)$,那么 $\overrightarrow{PA}\cdot\left( \overrightarrow{PB}+\overrightarrow{PC} \right)=\left( -x,-y\right)\cdot \left( 7-2x,4-2y \right)=2{{x}^{2}}-7x+2{{y}^{2}}-4y=2{{\left( x-\dfrac{7}{4}\right)}^{2}}+2{{\left( y-1 \right)}^{2}}-\dfrac{65}{8}$.即 $\overrightarrow{PA}\cdot(\overrightarrow{PB}+\overrightarrow{PC})$ 的最小值是 $-\dfrac{65}{8}$.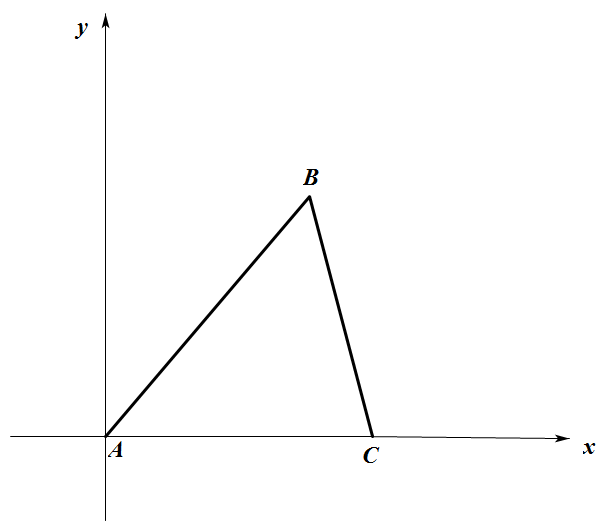

题目
答案
解析
备注