记 $A(0,0)$，$B(1,1)$，且 $d(P)$ 表示点 $P$ 到直线 $y=ax+b$ 的距离．
情形一当 $a\geqslant 2$ 或 $a\leqslant 0$ 时，有\[\begin{split}H(a,b)&=\max\left\{d(A),d(B)\right\}\\
&=\max\left\{\dfrac{|b|}{\sqrt{a^2+1}},\dfrac{|a+b-1|}{\sqrt{a^2+1}}\right\}\\
&\geqslant \dfrac 12\left(\dfrac{|b|}{\sqrt{a^2+1}}+\dfrac{|a+b-1|}{\sqrt{a^2+1}}\right)\\
&\geqslant \dfrac{|a-1|}{2\sqrt{a^2+1}}\\
&\geqslant \dfrac 1{2\sqrt 5}.\end{split}\]情形二当 $0<a<2$ 时，设函数图象上在点 $C$ 处的切线与直线 $y=ax+b$ 平行，则 $C\left(\dfrac a2,\dfrac {a^2}4\right)$，如图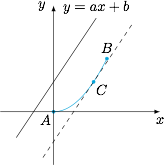．此时有\[H(a,b)=\max\left\{d(A),d(B),d(C)\right\}=\max\left\{\dfrac{|b|}{\sqrt{a^2+1}},\dfrac{|a+b-1|}{\sqrt{a^2+1}},\dfrac{\left|\dfrac {a^2}4+b\right|}{\sqrt{a^2+1}}\right\},\]从而\[\begin{cases}
H(a,b)\geqslant \dfrac 12\left(\dfrac{|b|}{\sqrt{a^2+1}}+\dfrac{\left|\dfrac {a^2}4+b\right|}{\sqrt{a^2+1}}\right),\\
H(a,b)\geqslant \dfrac 12\left(\dfrac{|a+b-1|}{\sqrt{a^2+1}}+\dfrac{\left|\dfrac {a^2}4+b\right|}{\sqrt{a^2+1}}\right),
\end{cases}\]进而\[\begin{cases}
H(a,b)\geqslant \dfrac{a^2}{8\sqrt{a^2+1}},\\
H(a,b)\geqslant \dfrac{(2-a)^2}{8\sqrt{a^2+1}},
\end{cases}\]当 $a>1$ 时，有\[H(a,b)\geqslant \dfrac{a^2}{8\sqrt{a^2+1}}=\dfrac{a}{8\sqrt{1+\dfrac{1}{a^2}}}>\dfrac{1}{8\sqrt 2}, \]当 $a<1$ 时，有\[H(a,b)\geqslant \dfrac{(2-a)^2}{8\sqrt{a^2+1}}=\dfrac{2-a}{8\sqrt{\left(\dfrac{a}{2-a}\right)^2+\dfrac{1}{(2-a)^2}}}>\dfrac{1}{8\sqrt 2},\]当 $a=1$ 时，有 $H(a,b)\geqslant \dfrac{\sqrt 2}{16}$，且当 $b=-\dfrac 18$ 时可以取得等号，于是 $H(a,b)$ 的最小值为 $\dfrac{\sqrt 2}{16}$．
综上所述，所求的最小值为 $\dfrac{\sqrt 2}{16}$．