函数 $f(x)=\sin (\pi x)$，$g(x)=\begin{cases} \dfrac{1}{2-2x},&x\ne 1,\\ 0,&x=1,\end{cases}$，则函数 $h(x)=f(x)-g(x),x\in (-2,4]$ 的所有零点的和为 ．
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（二测）
【标注】
【答案】
$9$
【解析】
如图．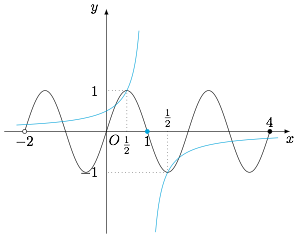
函数 $f(x)$ 和 $g(x)$ 的图象均关于点 $(1,0)$ 对称，且注意到\[f\left(\dfrac 12\right)=g\left(\dfrac 12\right)=1,\]于是函数 $h(x)$ 的零点共有 $9$ 个，因此所有零点的和为 $9$．
函数 $f(x)$ 和 $g(x)$ 的图象均关于点 $(1,0)$ 对称，且注意到\[f\left(\dfrac 12\right)=g\left(\dfrac 12\right)=1,\]于是函数 $h(x)$ 的零点共有 $9$ 个，因此所有零点的和为 $9$．
题目
答案
解析
备注
