如图，在平面直角坐标系 $xOy$ 中，$F$ 是椭圆 $\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1$（$a>b>0$）的右焦点，直线 $y=\dfrac {b}{2}$ 与椭圆交于 $B$，$C$ 两点，且 $\angle {BFC}=90^{\circ}$，则椭圆的离心率是 ．
【难度】
【出处】
2016年高考江苏卷
【标注】
【答案】
$\dfrac {\sqrt 6}{3}$
【解析】
根据椭圆的对称性，结合直角三角形斜边上的中线是斜边的一半列式求解即可．设椭圆的焦距为 $2c$，$BC$ 与 $y$ 轴的交点为 $D$，连接 $ DF $．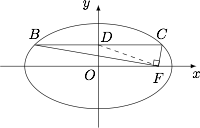
则 $D\left(0,\dfrac b2\right)$，$C\left(\dfrac {\sqrt 3}{2}a,\dfrac b2\right)$，$F\left(c,0\right)$．
因为 $\angle BFC=90^\circ $，$D$ 为 $BC$ 的中点，所以 $CD=DF$，所以\[c^2+\dfrac {b^2}{4}=\dfrac 34a^2.\]又因为\[b^2=a^2-c^2,\]所以 $\dfrac {c^2}{a^2}=\dfrac 23$．
所以椭圆的离心率为 $e=\dfrac ca=\dfrac {\sqrt 6}{3}$．
则 $D\left(0,\dfrac b2\right)$，$C\left(\dfrac {\sqrt 3}{2}a,\dfrac b2\right)$，$F\left(c,0\right)$．因为 $\angle BFC=90^\circ $，$D$ 为 $BC$ 的中点，所以 $CD=DF$，所以\[c^2+\dfrac {b^2}{4}=\dfrac 34a^2.\]又因为\[b^2=a^2-c^2,\]所以 $\dfrac {c^2}{a^2}=\dfrac 23$．
所以椭圆的离心率为 $e=\dfrac ca=\dfrac {\sqrt 6}{3}$．
题目
答案
解析
备注
