设 ${F_1},{F_2}$ 是双曲线 $C:\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\left(a > 0,b > 0\right)$ 的两个焦点，$ P $ 是 $ C $ 上一点，若 ${\left| {PF_1} \right| } + \left| {P{F_2}} \right| = 6a $，且 $\triangle P{F_1}{F_2}$ 的最小内角为 ${30^ \circ }$，则 $ C $ 的离心率为 ．
【难度】
【出处】
2013年高考湖南卷（理）
【标注】
【答案】
$\sqrt 3 $
【解析】
本题考查双曲线的定义和离心率的计算，以焦点三角形结合正余弦定理进行求解．如图，设 $ P $ 为右支上的点．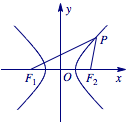
根据双曲线定义，可知\[|PF_1|-|PF_2|=2a,\]又 $|PF_1|+|PF_2|=6a$，可解得\[|PF_1|=4a,|PF_2|=2a,\]而 $|F_1F_2|=2c<2a$，所以 $\angle PF_1F_2$ 为最小内角，即\[\angle PF_1F_2=30^\circ,\]根据余弦定理，得\[\cos 30^{\circ}=\dfrac {{\left(4a\right)}^2+{\left(2c\right)}^2-{\left(2a\right)}^2} {2\cdot 4a \cdot 2c} \]解得，离心率$e=\dfrac c a =\sqrt 3$．
根据双曲线定义，可知\[|PF_1|-|PF_2|=2a,\]又 $|PF_1|+|PF_2|=6a$，可解得\[|PF_1|=4a,|PF_2|=2a,\]而 $|F_1F_2|=2c<2a$，所以 $\angle PF_1F_2$ 为最小内角，即\[\angle PF_1F_2=30^\circ,\]根据余弦定理，得\[\cos 30^{\circ}=\dfrac {{\left(4a\right)}^2+{\left(2c\right)}^2-{\left(2a\right)}^2} {2\cdot 4a \cdot 2c} \]解得，离心率$e=\dfrac c a =\sqrt 3$．
题目
答案
解析
备注
