点 $P$ 到点 $A\left(\dfrac 12,0\right),B(a,2)$ 及到直线 $x=-\dfrac 12$ 的距离都相等,如果这样的点恰好只有一个,那么 $a$ 的值是 .
【难度】
【出处】
无
【标注】
【答案】
$ \pm \dfrac{1}{2} $
【解析】
点 $P$ 到 $A$ 与 $P$ 到 $B$ 的距离相等,于是问题可以转化为线段 $AB$ 的垂直平分线 $l$ 与抛物线只有一个公共点,这包含两种情形.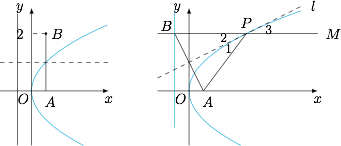
情形一 直线 $l$ 与抛物线的对称轴平行.如左图,此时 $l:y=1$,于是 $a=\dfrac 12$.
情形二 直线 $l$ 与抛物线相切.如右图,过 $P$ 作射线 $PM\parallel x$ 轴.根据抛物线的几何性质,$\angle 1=\angle 3$,因此 $\angle 1=\angle 2=\angle 3$,于是 $PB\parallel x$ 轴.因此 $P$ 点坐标为 $(2,2)$,进而$$PB=PA=2+\dfrac 12,$$解得 $a=-\dfrac 12$.
综合以上两种情形,$a=\pm \dfrac{1}{2}$.

综合以上两种情形,$a=\pm \dfrac{1}{2}$.
题目
答案
解析
备注