已知 $O$ 为坐标原点，$B(4,0)$，$C(5,0)$，过 $C$ 作 $x$ 轴的垂线，$M$ 是这垂线上的动点，以 $O$ 为圆心，$OB$ 为半径作圆，$MT_1,MT_2$ 是圆的切线，则 $\triangle{MT_1T_2}$ 垂心的轨迹方程是 ．
【难度】
【出处】
2011年全国高中数学联赛河北省预赛
【标注】
【答案】
$\left(x-\dfrac{16}{5}\right)^2+y^2=\dfrac{256}{25}$（$x>0$）
【解析】
如图．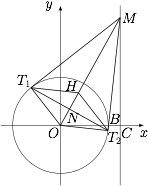
以 $O$ 为圆心，$OB$ 为半径的圆的方程为$$x^2+y^2=16.$$连接 $OT_1$，$OT_2$，$H$ 为 $\triangle{MT_1T_2}$ 的垂心，$N$ 为 $OM$ 与 $T_1T_2$ 的交点，易证四边形 $OT_2HT_1$ 是菱形，所以$$ON=\dfrac 12 OH.$$又$$OM\perp T_1T_2,OT_1\perp MT_1,$$则$$OT_1^2=ON\cdot OM.$$设点 $H$ 的坐标为 $(x,y)$，$M(5,b)$，则 $N\left(\dfrac x2,\dfrac y2\right)$，代入$$OT_1^2=ON\cdot OM,$$并有 $\dfrac b5=\dfrac yx$，得$$\left(x-\dfrac{16}{5}\right)^2+y^2=\left(\dfrac{16}{5}\right)^2,x>0$$为所求．
以 $O$ 为圆心，$OB$ 为半径的圆的方程为$$x^2+y^2=16.$$连接 $OT_1$，$OT_2$，$H$ 为 $\triangle{MT_1T_2}$ 的垂心，$N$ 为 $OM$ 与 $T_1T_2$ 的交点，易证四边形 $OT_2HT_1$ 是菱形，所以$$ON=\dfrac 12 OH.$$又$$OM\perp T_1T_2,OT_1\perp MT_1,$$则$$OT_1^2=ON\cdot OM.$$设点 $H$ 的坐标为 $(x,y)$，$M(5,b)$，则 $N\left(\dfrac x2,\dfrac y2\right)$，代入$$OT_1^2=ON\cdot OM,$$并有 $\dfrac b5=\dfrac yx$，得$$\left(x-\dfrac{16}{5}\right)^2+y^2=\left(\dfrac{16}{5}\right)^2,x>0$$为所求．
题目
答案
解析
备注
