如图1所示,在正方形 $ABCD$ 中,$E$ 是边 $AB$ 的中点.将 $\triangle DAE$ 和 $\triangle CBE$ 分别沿虚线 $DE$ 和 $CE$ 折起,使得 $AE$ 与 $BE$ 重合.记 $A$ 与 $B$ 重合后的点为 $P$(如图2所示),则平面 $PCD$ 与平面 $ECD$ 所成的二面角的大小为 .

【难度】
【出处】
全国高中数学联赛模拟试题(11)
【标注】
【答案】
$30^{\circ}$
【解析】
如图所示,过点 $P$ 作 $PF\perp CD$,联结 $EF$.由 $F$ 为 $CD$ 的中点,知 $EF\perp CD$,故 $\angle PFE$ 是平面 $CDE$ 与平面 $PCD$ 所成的二面角的平面角.
设正方形 $ ABCD $ 的边长为 $ a $,则 $ PE=DF=\frac{1}{2}a,PD=PC=EF=a $,$$ PF=\sqrt{PD^2-DF^2}=\sqrt{a^2-\left(\frac{1}{2}a\right)^2}=\frac{\sqrt{3}}{2}a.$$故$$ \cos\angle PEF=\frac{PF^2+EF^2-PE^2}{2PF\cdot EF}=\frac{\sqrt{3}}{2},\angle PFE=30^{\circ}.$$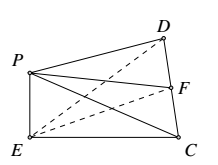
设正方形 $ ABCD $ 的边长为 $ a $,则 $ PE=DF=\frac{1}{2}a,PD=PC=EF=a $,$$ PF=\sqrt{PD^2-DF^2}=\sqrt{a^2-\left(\frac{1}{2}a\right)^2}=\frac{\sqrt{3}}{2}a.$$故$$ \cos\angle PEF=\frac{PF^2+EF^2-PE^2}{2PF\cdot EF}=\frac{\sqrt{3}}{2},\angle PFE=30^{\circ}.$$

题目
答案
解析
备注