如图，在棱长为 $1$ 的正方体 $ABCD-A_1B_1C_1D_1$ 中，若点 $E,F$ 分别为线段 $BD_1,CB_1$ 上的动点，点 $G$ 为底面 $ABCD$ 上的动点，则 $EF+EG$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 23$
【解析】
解决多个动点的最值问题，通常是先确定一部分点去考虑其他动点的最佳位置，然后调整之前暂时确定的点的位置，去研究整体的最佳状态，这种方法称为局部调整法．
在本题中，当 $E$ 点确定时，最好的 $G,F$ 点分别满足 $EG\perp ABCD$ 以及 $EF\perp B_1C$，于是 $F$ 是 $B_1C$ 的中点，且 $G$ 为 $E$ 在 $BD$ 上的投影，如图．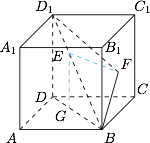
于是只需要将 $\triangle D_1FB$ 绕 $BD_1$ 旋转至与 $\triangle BDD_1$ 共面，然后过 $F$ 作 $BD$ 边上的垂线即得 $EF+EG$ 的最小值．为了方便，我们直接旋转 $\triangle D_1C_1B$，如图．
这样就由 $\cos\angle DBD_1=\sqrt{\dfrac 23}$ 得到 $\cos\angle C_1BD=2\cos^2\angle DBD_1-1=\dfrac 13$，于是$$FH=\sin\angle C_1BD\cdot FB=\dfrac{2\sqrt 2}3\cdot \dfrac{\sqrt 2}2=\dfrac 23,$$也即 $EF+EG$ 的最小值为 $\dfrac 23$．
在本题中，当 $E$ 点确定时，最好的 $G,F$ 点分别满足 $EG\perp ABCD$ 以及 $EF\perp B_1C$，于是 $F$ 是 $B_1C$ 的中点，且 $G$ 为 $E$ 在 $BD$ 上的投影，如图．
于是只需要将 $\triangle D_1FB$ 绕 $BD_1$ 旋转至与 $\triangle BDD_1$ 共面，然后过 $F$ 作 $BD$ 边上的垂线即得 $EF+EG$ 的最小值．为了方便，我们直接旋转 $\triangle D_1C_1B$，如图．这样就由 $\cos\angle DBD_1=\sqrt{\dfrac 23}$ 得到 $\cos\angle C_1BD=2\cos^2\angle DBD_1-1=\dfrac 13$，于是$$FH=\sin\angle C_1BD\cdot FB=\dfrac{2\sqrt 2}3\cdot \dfrac{\sqrt 2}2=\dfrac 23,$$也即 $EF+EG$ 的最小值为 $\dfrac 23$．
题目
答案
解析
备注
