已知正方体各个面的中心,甲、乙分别相互独立地从这 $6$ 个点中取出 $3$ 个,构成的两个三角形全等的概率是 .
【难度】
【出处】
2009年中国科学技术大学自主招生保送生测试
【标注】
【答案】
$\dfrac{13}{{25}}$
【解析】
如图,从这 $6$ 个点中取出 $3$ 个构成的三角形只有两种:等边三角形或等腰直角三角形.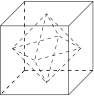
情形一 取出等边三角形.概率为 $\dfrac{8}{{{\rm{C}}_6^3}} = \dfrac{2}{5}$;
情形二 取出等腰直角三角形.概率为 $1 - \dfrac{2}{5} = \dfrac{3}{5}$;
于是所求概率为$${\left( {\dfrac{2}{5}} \right)^2} + {\left( {\dfrac{3}{5}} \right)^2} = \dfrac{{13}}{{25}}.$$

于是所求概率为$${\left( {\dfrac{2}{5}} \right)^2} + {\left( {\dfrac{3}{5}} \right)^2} = \dfrac{{13}}{{25}}.$$
题目
答案
解析
备注