如图，在平面直角坐标系中，点 $A$ 在抛物线 $y={x^2}-2x+2$ 上运动，过点 $A$ 作 $AC \perp x$ 轴于点 $C$，以 $AC$ 为对角线作矩形 $ABCD$，连接则对角线 $BD$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$1$
【解析】
因为 $AC,BD$ 为矩形的对角线，所以 $AC=BD$．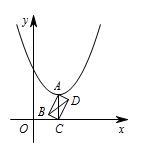
如图，当点 $A$ 为抛物线顶点时，$AC$ 最小．
而 $y={x^2}-2x+2=(x-1)^2+1$，
即此时 $AC=1$，
所以 $BD$ 的最小值为 $1$．
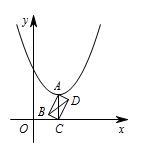如图，当点 $A$ 为抛物线顶点时，$AC$ 最小．而 $y={x^2}-2x+2=(x-1)^2+1$，
即此时 $AC=1$，
所以 $BD$ 的最小值为 $1$．
题目
答案
解析
备注
