已知非零向量 $\overrightarrow a$ 和 $\overrightarrow b$ 互相垂直，则 $\overrightarrow a+ \overrightarrow b$ 和 $\overrightarrow a+2\overrightarrow b$ 的夹角余弦值的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{2\sqrt 2}{3}$
【解析】
如图，不妨取 $|\overrightarrow{b}|=2$，设 $\overrightarrow {OA}=\overrightarrow {AB}=\overrightarrow b$，$\overrightarrow{OP}=\overrightarrow a+\overrightarrow b$，$\overrightarrow{OQ}=\overrightarrow a+2\overrightarrow b$，且 $OA=AB=2$，取线段 $AB$ 的中点 $M$．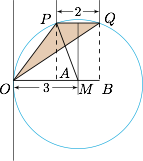
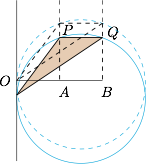
由圆的等张角性可知，当三角形 $OPQ$ 的外接圆与 $\overrightarrow a$ 的基线相切于 $O$ 点时 $\angle POQ$ 最大，此时容易求得$$\cos\angle POQ=\dfrac{\sqrt{PM^2-\left(\dfrac 12PQ\right)^2}}{PM}=\dfrac{2\sqrt2}{3}.$$否则当线段 $PQ$ 上下平移时，$O$ 点在圆的外部，对应的张角 $\angle POQ$ 会变小，如图．
由圆的等张角性可知，当三角形 $OPQ$ 的外接圆与 $\overrightarrow a$ 的基线相切于 $O$ 点时 $\angle POQ$ 最大，此时容易求得$$\cos\angle POQ=\dfrac{\sqrt{PM^2-\left(\dfrac 12PQ\right)^2}}{PM}=\dfrac{2\sqrt2}{3}.$$否则当线段 $PQ$ 上下平移时，$O$ 点在圆的外部，对应的张角 $\angle POQ$ 会变小，如图．
题目
答案
解析
备注
