如图，已知正方形 $ABCD$ 的边长为 $2$，点 $E$ 为 $AB$ 的中点．以 $A$ 为圆心，$AE$ 为半径，作弧交 $AD$ 于点 $F$．若 $P$ 为劣弧 $EF$ 上的动点，则 $\overrightarrow{PC}\cdot\overrightarrow{PD}$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$5-2\sqrt 5$
【解析】
我们熟知极化恒等式$$4\overrightarrow a\cdot\overrightarrow b=\left(\overrightarrow a+\overrightarrow b\right)^2-\left(\overrightarrow a-\overrightarrow b\right)^2,$$而注意到在本问题中向量 $\overrightarrow{PC}$ 与向量 $\overrightarrow{PD}$ 的差为定向量，于是$$4\overrightarrow{PC}\cdot\overrightarrow{PD}=\left(\overrightarrow{PC}+\overrightarrow{PD}\right)^2-\left(\overrightarrow{PC}-\overrightarrow{PD}\right)^2=\left(\overrightarrow{PC}+\overrightarrow{PD}\right)^2-4,$$取 $CD$ 的中点 $M$，则有$$\overrightarrow{PC}\cdot\overrightarrow{PD}=PM^2-1,$$如图．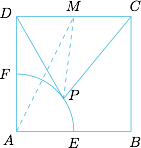
问题转化为求 $PM^2-1$ 的最小值，显然当 $A$、$P$、$M$ 三点共线时，$PM^2-1$ 取得最小值$$\left(AM-1\right)^2-1=\left(\sqrt 5-1\right)^2-1=5-2\sqrt 5.$$
问题转化为求 $PM^2-1$ 的最小值，显然当 $A$、$P$、$M$ 三点共线时，$PM^2-1$ 取得最小值$$\left(AM-1\right)^2-1=\left(\sqrt 5-1\right)^2-1=5-2\sqrt 5.$$
题目
答案
解析
备注
