若存在实数 $a$ 使得 $|x+a|\leqslant \ln x+1$ 在 $x\in [1,m]$ 上恒成立,则 $m$ 的最大正整数值为 .
【难度】
【出处】
无
【标注】
【答案】
$4$
【解析】
参数 $a$ 的值控制着函数 $y=|x+a|$ 的图象的左右移动.因此当 $-a$ 增大时,对应的 $m$ 也相应增大.当 $y=|x+a|$ 的"左翼"过 $y=\ln x+1$ 上的点 $(1,1)$ 时,$-a$ 最大,此时使得题中不等式成立的范围的"上限"最大,如图.不难求得 $m$ 的最大正整数值为 $4$.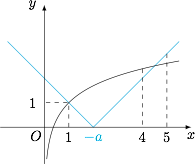

题目
答案
解析
备注