已知函数 $y = f\left(x\right)\left(x \in{\mathbb{R}}\right)$．对函数 $y = g\left(x\right)\left(x \in I\right)$，定义 $g\left(x\right)$ 关于 $f\left(x\right)$ 的"对称函数"为函数 $y = h\left(x\right)\left(x \in I\right)$，$y = h\left(x\right)$ 满足：对任意 $x \in I$，两个点 $\left(x,h\left(x\right)\right)$，$\left(x,g\left(x\right)\right)$ 关于点 $\left(x,f\left(x\right)\right)$ 对称．若 $h\left(x\right)$ 是 $g\left(x\right) = \sqrt{4 -{x^2}}$ 关于 $f\left(x\right) = 3x + b$ 的"对称函数"，且 $h\left(x\right) > g\left(x\right)$ 恒成立，则实数 $b$ 的取值范围是 ．
【难度】
【出处】
2014年高考山东卷（理）
【标注】
【答案】
$\left(2\sqrt{10},+\infty \right)$
【解析】
根据对称函数的定义，函数 $h(x)$ 与 $g(x)$ 的图象分别在 $f(x)$ 的图象的两侧．由于 $y=\sqrt{4-x^2}$ 即 $x^2+y^2=4$（$y\geqslant 0$），因此 $g(x)$ 的图象是一个半圆，而 $f(x)$ 的图象是一条直线，所以当直线 $y=3x+b$ 在半圆 $y=\sqrt{4-x^2}$ 上方时符合题意．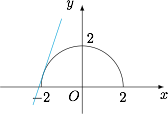
此时有$$\dfrac{|b|}{\sqrt{1^2+3^2}}>2,\land b>0,$$解得 $b>2\sqrt{10}$．
此时有$$\dfrac{|b|}{\sqrt{1^2+3^2}}>2,\land b>0,$$解得 $b>2\sqrt{10}$．
题目
答案
解析
备注
