梯形 $ABCD$ 中 $AB\parallel CD$，对角线 $AC,BD$ 交于 $P_1$，过 $P_1$ 作 $AB$ 的平行线交 $BC$ 于点 $Q_1$．$AQ_1$ 交 $BD$ 于 $P_2$，过 $P_2$ 作 $AB$ 的平行线交 $BC$ 于点 $Q_2$，$\cdots $．若 $AB=a$，$CD=b$，则 $P_nQ_n=$ （用 $a,b,n$ 表示）．
【难度】
【出处】
2016年中国科学技术大学自主招生试题
【标注】
【答案】
$\dfrac{ab}{a+bn}$
【解析】
如图．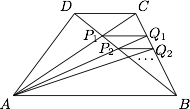
设 $P_nQ_n=x_n$（$n\in\mathbb N$），则 $x_0=CD=b$，且$$\dfrac{1}{x_n}=\dfrac{1}{x_{n-1}}+\dfrac 1a,$$于是可得 $\dfrac{1}{x_n}=\dfrac na+\dfrac{1}{x_0}$，即 $x_n=\dfrac{ab}{a+bn}$（$n\in\mathbb N$）．
设 $P_nQ_n=x_n$（$n\in\mathbb N$），则 $x_0=CD=b$，且$$\dfrac{1}{x_n}=\dfrac{1}{x_{n-1}}+\dfrac 1a,$$于是可得 $\dfrac{1}{x_n}=\dfrac na+\dfrac{1}{x_0}$，即 $x_n=\dfrac{ab}{a+bn}$（$n\in\mathbb N$）．
题目
答案
解析
备注
