在平面四边形 $ABCD$ 中，$\angle A=\angle B=\angle C=75^\circ$，$BC=2$，则 $AB$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$
【解析】
如图，作底角为 $75^\circ$ 的等腰三角形 $NBC$，使 $BC=2$，过 $C$ 作直线 $CM$ 交 $NB$ 于 $M$，使 $\angle BMC=75^\circ$．由图可知 $A$ 在线段 $MN$ 上运动（不包括两个端点）．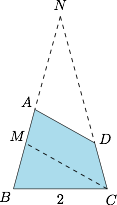
在等腰三角形 $CBM$ 中，由$$BM=4\cos 75^\circ=\sqrt 6-\sqrt 2,$$进而由三角形 $NBC$ 与三角形 $CBM$ 相似，有$$BC^2=BM\cdot BN,$$得$$BN=\sqrt 6+\sqrt 2,$$从而 $AB$ 的取值范围是 $\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$．
在等腰三角形 $CBM$ 中，由$$BM=4\cos 75^\circ=\sqrt 6-\sqrt 2,$$进而由三角形 $NBC$ 与三角形 $CBM$ 相似，有$$BC^2=BM\cdot BN,$$得$$BN=\sqrt 6+\sqrt 2,$$从而 $AB$ 的取值范围是 $\left(\sqrt 6-\sqrt 2,\sqrt 6+\sqrt 2\right)$．
题目
答案
解析
备注
