若点 $A$ 在圆 $C:(x-1)^2+(y+2)^2=4$ 上运动，点 $B$ 在 $y$ 轴上运动，则对定点 $P(3,2)$ 而言，$\left|\overrightarrow {PA}+\overrightarrow {PB}\right|$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
解决问题的关键是将所求两个向量的和转化为一个向量，以方便研究它的长度．
平行四边形法则 取线段 $AB$ 的中点 $M$，则$$\overrightarrow {PA}+\overrightarrow {PB}=2\overrightarrow {PM},$$于是问题转化为求向量 $\overrightarrow {PM}$ 长度最大值的两倍．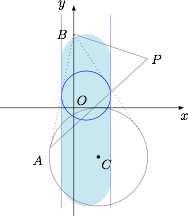
接下来的问题就是思考 $M$ 的轨迹．不妨先固定点 $B$，这样 $M$ 的轨迹就是一个半径为 $1$ 的圆，然后再让 $B$ 点在 $y$ 轴上动起来，这样 $M$ 的轨迹就是在两条平行直线间的部分，如图（也可以先固定 $A$ 点）．
这样我们就得到了所求的最小值为 $3$．
三角形法则 作 $B$ 点关于 $P$ 点的对称点 $B'$，则$$\overrightarrow {PA}+\overrightarrow {PB}=\overrightarrow {PA}-\overrightarrow {PB'}=\overrightarrow {B'A},$$于是问题转化问求向量 $\overrightarrow {B'A}$ 长度的最小值．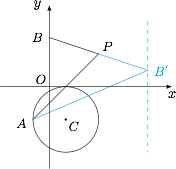
事实上，$B'$ 的轨迹是 $y$ 轴关于 $P$ 点对称的直线 $x=6$，于是问题转化成了圆 $C$ 上的点到直线 $x=6$ 的距离的最小值，不难求得为 $3$．
当然，也可以作 $A$ 点关于 $P$ 点的对称点，本质相同．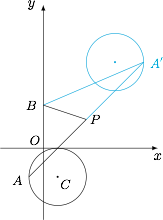
接下来的问题就是思考 $M$ 的轨迹．不妨先固定点 $B$，这样 $M$ 的轨迹就是一个半径为 $1$ 的圆，然后再让 $B$ 点在 $y$ 轴上动起来，这样 $M$ 的轨迹就是在两条平行直线间的部分，如图（也可以先固定 $A$ 点）．这样我们就得到了所求的最小值为 $3$．
事实上，$B'$ 的轨迹是 $y$ 轴关于 $P$ 点对称的直线 $x=6$，于是问题转化成了圆 $C$ 上的点到直线 $x=6$ 的距离的最小值，不难求得为 $3$．当然，也可以作 $A$ 点关于 $P$ 点的对称点，本质相同．
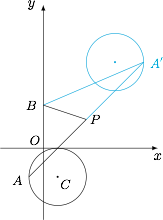
题目
答案
解析
备注
