已知点集 $M=\left\{(x,y)\left|\sqrt{1-x^2}\cdot\sqrt{1-y^2}\geqslant xy\right.\right\}$,则平面直角坐标系中区域 $M$ 的面积为 .
【难度】
【出处】
2015年北京大学博雅计划数学试卷
【标注】
【答案】
$2+\dfrac{\pi}2$
【解析】
如图.当 $xy\leqslant 0$ 时,只需要满足 $x^2\leqslant 1,y^2\leqslant 1$ 即可;
当 $xy>0$ 时,对不等式两边平方整理得 $x^2+y^2\leqslant 1$,所以区域 $M$ 如下图: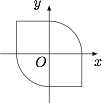
当 $xy>0$ 时,对不等式两边平方整理得 $x^2+y^2\leqslant 1$,所以区域 $M$ 如下图:

题目
答案
解析
备注