定义区间 $(a,b)$，$[a,b)$，$(a,b]$，$[a,b]$ 的长度均为 $d=b-a$，多个区间并集的长度为各区间长度之和，例如 $(1,2)\cup [3,5)$ 的长度 $d=(2-1)+(5-3)=3$．设 $f(x)=[x]\cdot \{x\}$，$g(x)=x-1$，其中 $[x]$ 表示不超过 $x$ 的最大整数，$\{x\}=x-[x]$．若用 $d_1$、$d_2$、$d_3$ 分别表示不等式 $f(x)>g(x)$、方程 $f(x)=g(x)$、不等式 $f(x)<g(x)$ 解集区间的长度，则当 $-2016\leqslant x\leqslant 2016$ 时，$d_1=$ ；$d_2=$ ；$d_3=$ ．
【难度】
【出处】
无
【标注】
【答案】
$2017$；$1$；$2014$
【解析】
用图形语言解决，我们已知熟悉函数 $y=[x]$ 与 $y=\{x\}$ 的图象，于是得到 $f(x)$ 的图象，将它与 $g(x)$ 的图象同时画出，如下：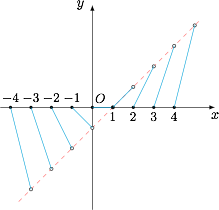
由图象知当 $x<1$ 时，$f(x)>g(x)$；当 $1\leqslant x<2$ 时，$f(x)=g(x)$；当 $x\geqslant 2$ 时，$f(x)<g(x)$．
从多个角度分析同一个对象，会让我们对它的理解更加全面深刻，从而对于与它相关的各种问题都能通过尝试找到一条可行的路．
由图象知当 $x<1$ 时，$f(x)>g(x)$；当 $1\leqslant x<2$ 时，$f(x)=g(x)$；当 $x\geqslant 2$ 时，$f(x)<g(x)$．从多个角度分析同一个对象，会让我们对它的理解更加全面深刻，从而对于与它相关的各种问题都能通过尝试找到一条可行的路．
题目
答案
解析
备注
