设曲线 $y = \sqrt {2x - {x^2}} $ 与 $x$ 轴所围成的区域为 $D$，向区域 $D$ 内随机投一点，该点落在 $D$ 内任一小区域的概率只与该小区域的面积成比例，则该点落入区域 $\left\{ {\left( {x , y} \right) \in D\mid {x^2} + {y^2} < 2} \right\}$ 内的概率为 ．
【难度】
【出处】
2013年卓越大学联盟自主选拔录取学科基础测试数学试题
【标注】
【答案】
$1 - \dfrac{1}{{{\pi }}}$
【解析】
区域 $D$ 是半径为 $1$ 的半圆，如图，所求概率为阴影部分的面积比上半圆面积：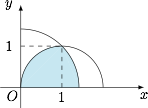
所以所求概率为$$P=\dfrac{\dfrac 12\left(\dfrac{\pi}2-1\right)+\dfrac{\pi}4}{\dfrac 12\pi}=1-\dfrac 1{\pi}.$$
所以所求概率为$$P=\dfrac{\dfrac 12\left(\dfrac{\pi}2-1\right)+\dfrac{\pi}4}{\dfrac 12\pi}=1-\dfrac 1{\pi}.$$
题目
答案
解析
备注
