已知 $\triangle ABC$ 中，$\angle A = {90^ \circ }$，$BC = 4$，点 $A$ 是线段 $EF$ 的中点，$EF = 2$，若 $\overrightarrow {EF} $ 与 $\overrightarrow {BC} $ 的夹角为 ${60^ \circ }$，则 $\overrightarrow {BE} \cdot \overrightarrow {CF} {{ = }}$ ．
【难度】
【出处】
2012年卓越人才培养合作高校自主选拔学业能力测试数学试题
【标注】
【答案】
$1$
【解析】
先考虑特殊的情况，设 $\angle B = \dfrac{{{\pi }}}{3}$，于是 $E$ 为线段 $BA$ 的中点．如图所示：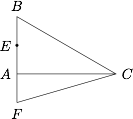
于是$$\overrightarrow {BE} \cdot \overrightarrow {CF} = \overrightarrow {AF} \cdot \overrightarrow {CF} = {\left| {\overrightarrow {AF} } \right|^2} = 1.$$下面考虑一般的情形．如图所示：
\[\begin{split}\overrightarrow {BE} \cdot \overrightarrow {CF} & = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right) \cdot \left( {\overrightarrow {CA} + \overrightarrow {AF} } \right)\\& = \overrightarrow {BA} \cdot \overrightarrow {CA} + \overrightarrow {BA} \cdot \overrightarrow {AF} + \overrightarrow {AE} \cdot \overrightarrow {CA} + \overrightarrow {AE} \cdot \overrightarrow {AF} \\& = 0 + \overrightarrow {AE} \cdot \left( {\overrightarrow {CA} - \overrightarrow {BA} } \right) - 1\\& = - 1 + \overrightarrow {AE} \cdot \overrightarrow {CB} \\&= - 1 + 1 \cdot 4 \cdot \dfrac{1}{2} = 1.\end{split}\]
于是$$\overrightarrow {BE} \cdot \overrightarrow {CF} = \overrightarrow {AF} \cdot \overrightarrow {CF} = {\left| {\overrightarrow {AF} } \right|^2} = 1.$$下面考虑一般的情形．如图所示：\[\begin{split}\overrightarrow {BE} \cdot \overrightarrow {CF} & = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right) \cdot \left( {\overrightarrow {CA} + \overrightarrow {AF} } \right)\\& = \overrightarrow {BA} \cdot \overrightarrow {CA} + \overrightarrow {BA} \cdot \overrightarrow {AF} + \overrightarrow {AE} \cdot \overrightarrow {CA} + \overrightarrow {AE} \cdot \overrightarrow {AF} \\& = 0 + \overrightarrow {AE} \cdot \left( {\overrightarrow {CA} - \overrightarrow {BA} } \right) - 1\\& = - 1 + \overrightarrow {AE} \cdot \overrightarrow {CB} \\&= - 1 + 1 \cdot 4 \cdot \dfrac{1}{2} = 1.\end{split}\]
题目
答案
解析
备注
