设 $\triangle ABC$，${P_0}$ 是边 $AB$ 上一定点，满足 ${P_0}B = \dfrac{1}{4}AB$，且对于边 $AB$ 上任一点 $P$，恒有 $\overrightarrow {PB} \cdot \overrightarrow {PC} \geqslant \overrightarrow {{P_0}B} \cdot \overrightarrow {{P_0}C} $，则 \((\qquad)\)
【难度】
【出处】
2013年高考浙江卷（理）
【标注】
【答案】
D
【解析】
本题注意到 $\left|\overrightarrow{CB}\right|$ 是定值，所以可以把 $\overrightarrow{PB}\cdot \overrightarrow{PC}$ 化为 $\dfrac 14\left[\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\left(\overrightarrow{PB}-\overrightarrow{PC}\right)^2\right]$，然后求 $\overrightarrow{PB}+\overrightarrow{PC}$ 的模长的最小值即可．由题意知，$P$ 为边 $AB$ 上的动点，$\overrightarrow{PB}\cdot \overrightarrow{PC}$ 取到最小值时，点 $P$ 的位置为 $AB$ 靠近 $B$ 的四等分点．
因为\[\begin{split}\overrightarrow{PB}\cdot \overrightarrow{PC}&=\dfrac 14\left[\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\left(\overrightarrow{PB}-\overrightarrow{PC}\right)^2\right]
\\&=\dfrac 14\left[\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\overrightarrow{CB}\cdot\overrightarrow{CB}\right].\end{split}\]（推导中用到：）
所以只需求 $\overrightarrow{PB}+\overrightarrow{PC}$ 的模长的最小值，如图，作 $\overrightarrow{B'P}=\overrightarrow{PB}$，则 $\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{B'C}$，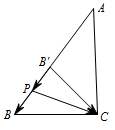
显然，当 $B'C\perp AB$ 时，满足题意，而 $B'$ 恰为 $AB$ 的中点，故有 $AC=BC$．
其他方法：
设 $\overrightarrow{PB}=\lambda\overrightarrow{AB}$，则\[\begin{split}\overrightarrow{PB}\cdot\overrightarrow{PC}&=\lambda\overrightarrow{AB}\cdot\left(\lambda\overrightarrow{AB}+\overrightarrow{BC}\right)
\\&=\left(\overrightarrow{AB}\cdot\overrightarrow{AB}\right)\lambda^2+\left(\overrightarrow{AB}\cdot\overrightarrow{BC}\right)\lambda.\end{split}\]（推导中用到：）
于是当 $\lambda=-\dfrac{\overrightarrow{AB}\cdot\overrightarrow{BC}}{2\overrightarrow{AB}\cdot\overrightarrow{AB}}=\dfrac 14$ 时，$\overrightarrow{PB}\cdot\overrightarrow{PC}$ 有最小值，得到 $\cos B=\dfrac{AB}{2BC}$，数形结合或由余弦定理都可以得到 $AC=BC$．
因为\[\begin{split}\overrightarrow{PB}\cdot \overrightarrow{PC}&=\dfrac 14\left[\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\left(\overrightarrow{PB}-\overrightarrow{PC}\right)^2\right]
\\&=\dfrac 14\left[\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\overrightarrow{CB}\cdot\overrightarrow{CB}\right].\end{split}\]（推导中用到：）
所以只需求 $\overrightarrow{PB}+\overrightarrow{PC}$ 的模长的最小值，如图，作 $\overrightarrow{B'P}=\overrightarrow{PB}$，则 $\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{B'C}$，
显然，当 $B'C\perp AB$ 时，满足题意，而 $B'$ 恰为 $AB$ 的中点，故有 $AC=BC$．其他方法：
设 $\overrightarrow{PB}=\lambda\overrightarrow{AB}$，则\[\begin{split}\overrightarrow{PB}\cdot\overrightarrow{PC}&=\lambda\overrightarrow{AB}\cdot\left(\lambda\overrightarrow{AB}+\overrightarrow{BC}\right)
\\&=\left(\overrightarrow{AB}\cdot\overrightarrow{AB}\right)\lambda^2+\left(\overrightarrow{AB}\cdot\overrightarrow{BC}\right)\lambda.\end{split}\]（推导中用到：）
于是当 $\lambda=-\dfrac{\overrightarrow{AB}\cdot\overrightarrow{BC}}{2\overrightarrow{AB}\cdot\overrightarrow{AB}}=\dfrac 14$ 时，$\overrightarrow{PB}\cdot\overrightarrow{PC}$ 有最小值，得到 $\cos B=\dfrac{AB}{2BC}$，数形结合或由余弦定理都可以得到 $AC=BC$．
题目
答案
解析
备注
